Vectors Work Sheet Name: _________________

1. Which of these vectors is the same (or equivalent)?

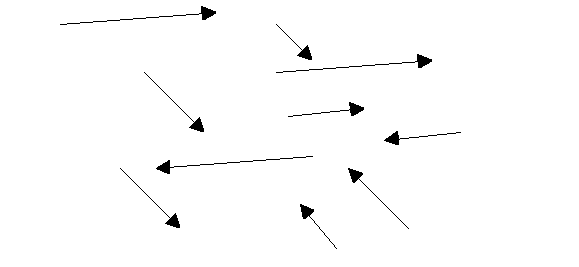
For one vector to be equivalent (or equal to another) what has to be true?___________________________________________________________________________________________________________

2. Name the end points for these vectors and write these vectors as ordered pairs

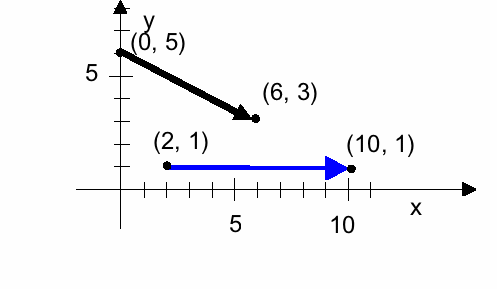
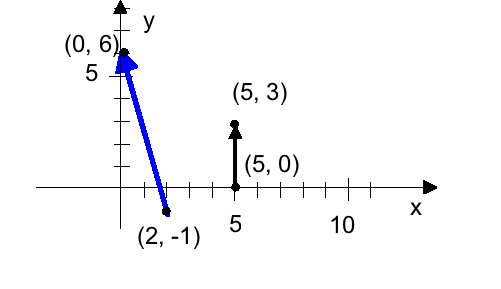
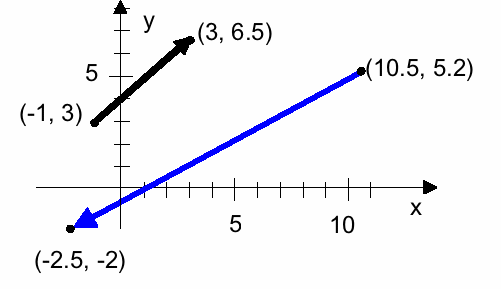
2. For each of the vectors above, write them also using unit vector notation (using 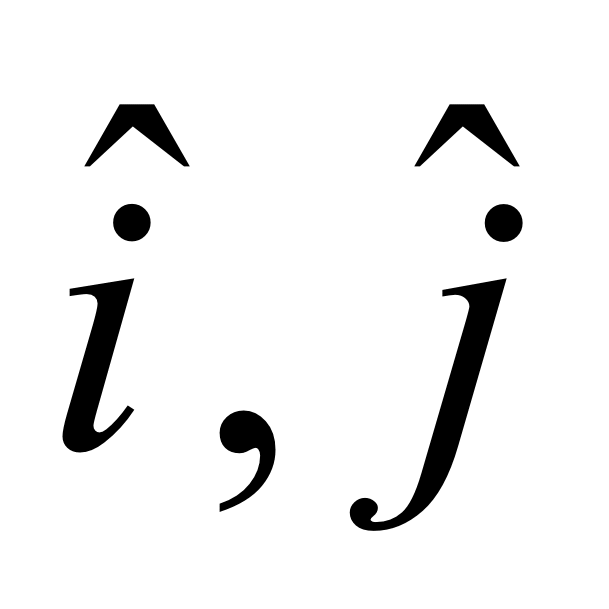notation).

2. A vector B = (7, -1, 9) the x-component is _________ the y-component is __________, and the z-component is ________

2. What is the magnitude of the vector v = (-1, -3)?

2. What angle does the vector v = (-1, -3) make with the positive x-axis?

2. In the diagram below, are the vectors A and B being added correctly?

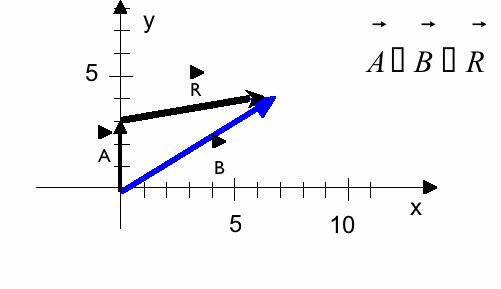
Draw the addition (and the resultant vector) as it should have been:

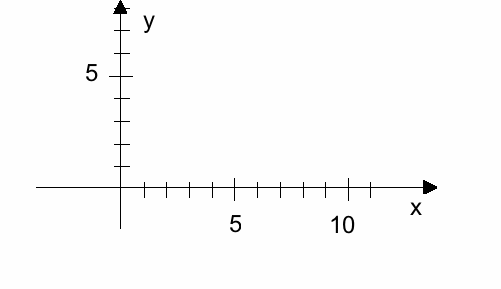
Does the resultant vector look the same? (It shouldn’t!)

8. Add these vectors, given their components:

Vector 1	Vector 2	Sum
(1, 1)	(3, 4)
(-1, 2, -4)	(5, 0, 2)
(0, 1, 0)	(1, 0, 0)
(2.4, -0.9)	(-1, 0.3)

9. Determine the x and y components of these vectors:

(Draw a sketch of each)

1. magnitude 9, angle 30^o with the positive x-axis.

2. Magnitude 11, angle -60^o with positive x-axis

3. Magnitude 60 m/s at an angle of 45^o above the x-axis

4. Magnitude 17 N/C at an angel of 115^o with the positive x-axis

9. Write each of your vectors in question 9 above in unit vector notation.

a)

b)

c)

d)

9. a) If the vector u = (-3, -4) has magnitude 5, what is the magnitude of the vector 2u?

2. What angle do each of these make with the positive x-axis?

2. Does multiplying a vector by a positive number change its direction?

2. Does multiplying a vector by a negative number change its direction?

9. If the vector u = (-3, -4), what is - u?

Write both in unit vector notation.

9. Do the vector subtraction:

Vector 1	Vector 2	Difference (vector 1 – vector 2)
(1, 1)	(3, 4)
(-1, 2, -4)	(5, 0, 2)
(0, 1, 0)	(1, 0, 0)
(2.4, -0.9)	(-1, 0.3)